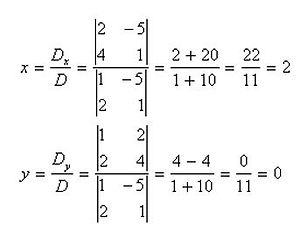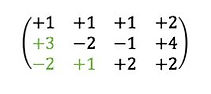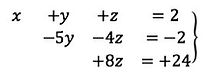El contenido de este sitio web esta propuesto para estudiantes desde el grado 9º hasta universitarios.
Menos usados y complejos
Regla de Cramer
La regla de Cramer proporciona la solución de sistemas de ecuaciones lineales compatibles determinados (con una única solución) mediante el cálculo de determinantes.
Se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones:
-
El número de ecuaciones es igual al número de incógnitas.
-
El determinante de la matriz de los coeficientes es distinto de cero.
-
Considere el sistema de dos ecuaciones lineales con dos variables:
ax + by = c
dx + ey = f
Usando el método de combinación lineal, puede verificar que:
si ae – bd ≠ 0
Dese cuenta que los denominadores son iguales al determinante de los coeficientes.
Los numeradores son iguales a los determinantes D x y D y donde
D x se forma reemplazando la columna de coeficientes de x en D con la columna de constantes y D y se forma reemplazando la columna de coeficientes de y en D con la columna de constantes.
Por sustitución,
Ejemplo:
Utilice determinantes para resolver el sistema de ecuaciones:
Por lo tanto, la solución es (2, 0).
Método de Gauss
El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales con sus filas la transformamos en una matriz triangular superior (o inferior). De esta forma obtenemos un sistema equivalente al inicial y que es muy fácil de resolver.
Ejemplo:
Utilizamos los coeficientes y los términos independientes y realizamos una matriz:
Necesitamos hacer ceros en los números destacados en la matriz anterior.
Primeras transformaciones, deseamos realizar los ceros de la primera columna:
Primer paso, transformar la segunda fila,
-
Fila uno multiplicada por -3
-3.(+1 +1 +1 +2)=-3 -3 -3 -6
-
Le sumo la fila 2.
Segundo paso, transformar la tercera fila,
-
Fila uno multiplicada por +2.
+2.(+1 + 1+1 +2 )=+2 +2 +2 +4
-
Le sumo la fila 3.
Así, la matriz resultante sería:
Segundas transformaciones, deseamos realizar el ceros de la segunda columna:
Para ello, sólo utilizamos la segunda y tercera fila:
-
Fila uno se mantiene.
-
Fila dos se multiplica por 3.
+3.(0 -5 -4 -2)=+0 -15 -12 -6
-
Fila tres se multiplica por 5.
+5.(0 +3 +4 +6)=0 +15 +20 +30
-
Sumo la fila dos y tres transformadas.
De esta manera, el sistema resulta:
Siendo la solución:
z=24/8=+3
z=+3
Sustituimos el valor de “z” en la segunda ecuación y obtenemos el valor de “y”:
-5y-4.3=-2
-5y=-2+12
y=+10/-5=-2
y=-2
Sustituimos el valor de “z” e “y” en la primera ecuación y obtenemos “x”:
x+(-2)+3=+2
x=+2-3+2
x=+1
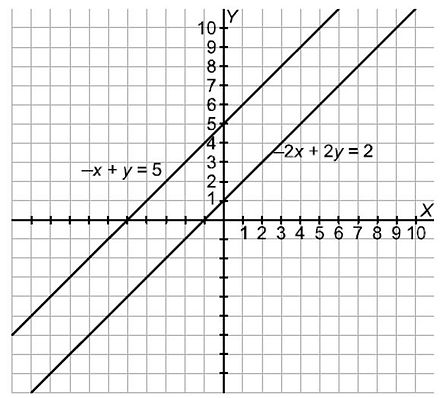
Método gráfico
Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión 2.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico esta dado en los siguientes pasos:
-
Se despeja la incógnita (y) en ambas ecuaciones.
-
Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.
-
Se representan gráficamente ambas rectas en los ejes coordenados.
-
En este último paso hay tres posibilidades:
-
Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas (x,y). "Sistema compatible determinado".
-
Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. «Sistema compatible indeterminado».
-
Si ambas rectas son paralelas, el sistema no tiene solución.
el sistema no tiene solución.